2020年10月，MDPI期刊Fractal and Fractional被Web of Science的Science Citation Index Expanded (SCIE)数据库收录。Fractal and Fractional向为期刊工作作出巨大贡献的主编与编委表示衷心的感谢。同时，Fractal and Fractional也衷心感谢各位作者、审稿人和读者的支持与信任！截至目前，MDPI出版的280余个期刊中，共有80个被SCIE数据库收录。

 

期刊介绍

 

Fractal and Fractional (ISSN 2504-3110) 创刊于2017年，是由MDPI组织出版的国际型开放获取期刊。期刊研究范围包括分形和分数阶微积分基础研究及其在不同科学和工程领域中的应用。目前，期刊编委会由来自世界各地的49名知名学者组成。创刊短短四年，期刊已相继被Scopus和Science Citation Index Expanded (SCIE) - Web of Science等重要数据库收录。Fractal and Fractional采用高标准单盲同行评审，平均一审周期为18.7天，文章从接收到发表仅需3.5天。

 

主编介绍

 

Prof. Dr. Carlo Cattani

 

自2017年创刊以来，Carlo Cattani教授一直担任Fractal and Fractional的主编，同时他还担任了多个重要国际学术期刊的编辑。Carlo Cattani教授目前在意大利托斯卡纳大学工程学院数学物理和应用数学系任职。他曾任职于意大利国家研究委员会 (1978-1980)，斯德哥尔摩大学物理研究所 (1987-1988)，罗马大学数学系 (1980-2004)，萨勒诺大学数学系 (2004-2015)。Carlo Cattani教授主要研究领域包括数值和计算方法，数学模型和方法，时间序列和数据分析，计算机方法和模拟。他在国际期刊上共发表了250多篇学术论文，Google Scholar H指数为45，出版过多部合著，在数值方法、动力系统、分数微积分、分形、小波、非线性波等基础课题上做出了巨大贡献。他于2020年10月被评选为世界排名前2%的科学家 (由斯坦福大学发布)，在数值和计算数学领域排名85 (意大利位列第2)。为表彰他在学术研究和国际合作方面的贡献，他被阿塞拜疆大学 (2019年)、俄罗斯巴什基尔国立大学 (2009年) 授予荣誉教授称号，被越南孙德盛大学 (2018年) 聘请为客座教授。

 

文章推荐

 

Rotationally Symmetric Lacunary Functions and Products of Centered Polygonal Lacunary Functions

旋转对称缺项函数与中心多边形缺项函数的乘积

L. K. Mork et al.

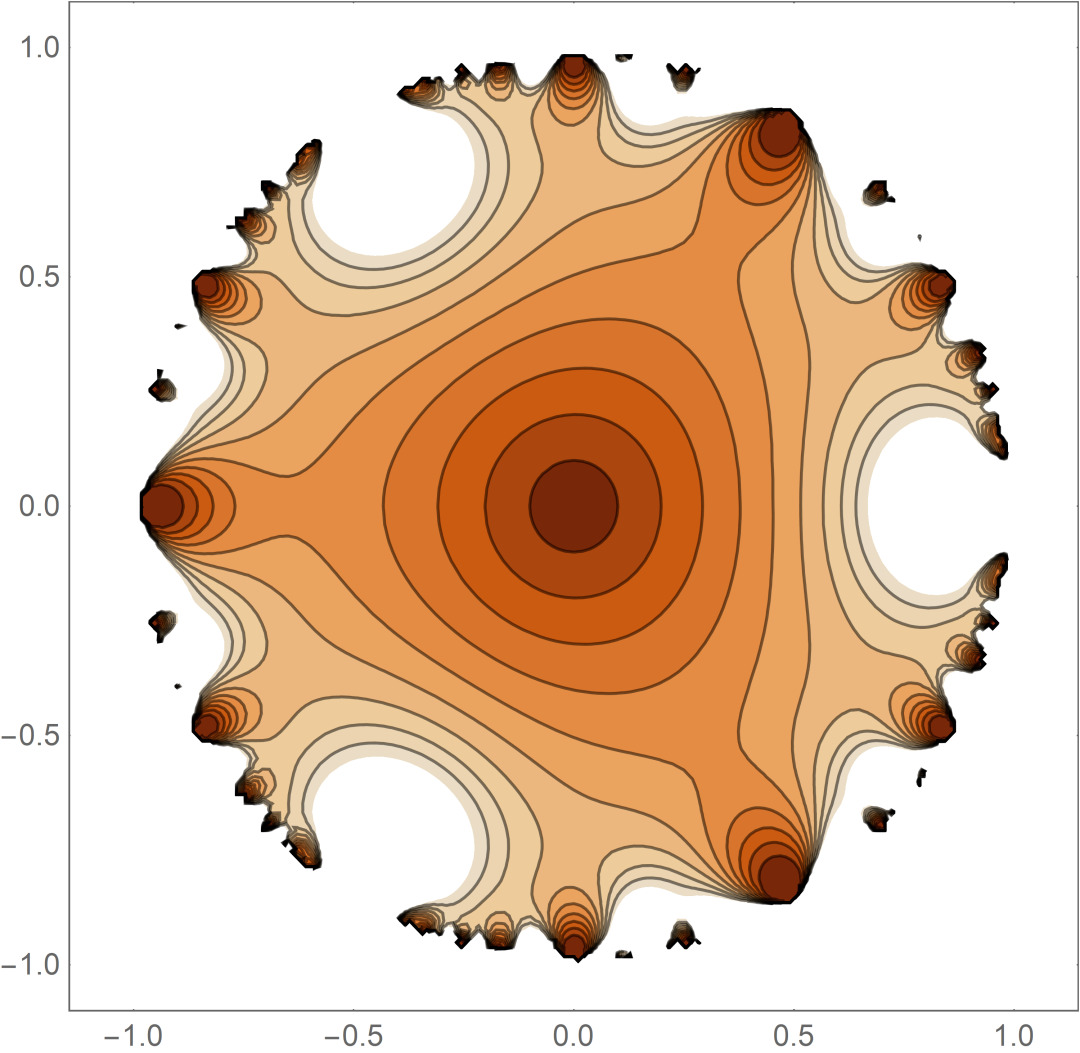
解析函数是数学追求的丰富而美丽的领域，也是物理学中用来洞察无数自然现象的最强大的工具之一。其中，较少被探索的解析函数是那些具有被称为自然边界的奇异曲线的函数，特别是缺项函数。最近，缺项函数已经被用于解决物理问题。本文在先前对中心多边形缺项函数研究的基础上，通过定理证明了这些缺项函数在模水平上是如何呈现旋转和二面镜对称的。这些定理为构建其他具有相同对称性的缺项函数提供了一个总体框架。这些研究使我们能够更好地探索空白行为对相关缺项函数的定性特征的影响。进一步定义了有中心多边形缺项函数的两个重正化积，并通过几个定理与Ramanunjan三角缺失级数建立了联系。

访问后方链接，阅读英文原文：https://www.mdpi.com/2504-3110/4/2/24

 

Fractal, Scale Free Electromagnetic Resonance of a Single Brain Extracted Microtubule Nanowire, a Single Tubulin Protein and a Single Neuron

大脑提取的单个微管纳米线，单个微管蛋白和单个神经元的分形，无标度电磁共振

Komal Saxena et al.

近一个世纪以来，电磁共振和天线-接收机的特性已经被广泛测量和进行理论建模。生物材料的介电成分—如果以不同的对称排列，那么每一种振动对称—都会导致不同的共振频率。虽然有关蛋白质介电共振的文献资料丰富，但振动模式的无标度关系却很少见。本文中，作者报道了4纳米宽的微管蛋白、25纳米宽的微管纳米线和1-微米宽的神经元轴突起始段的三联体共振频率模式的自相似。因此，保持振动的对称性是三种材料集成的基本特征。在物理外观上没有自相似性: 尺寸变化了106个级次，然而，当它们振动时，频率变化的比值使得三个共振频带中的每一个都包含了另外三个频带 (三联体中的三联(triplet of triplet))。这表明，自相似性取决于对称破缺原理，而不是对称。这就是为什么有三种元素，一种蛋白质，它是复杂的，神经元在106个不同的时域共振，但它们的振动频率组合相似。这项研究支持了已经存在的关于大脑中从分子到认知的无标度信息整合的假设。

访问后方链接，阅读英文原文：https://www.mdpi.com/2504-3110/4/2/11

 

Fractal Antennas: An Historical Perspective

分形天线：历史回顾与展望

Jaume Anguera et al.

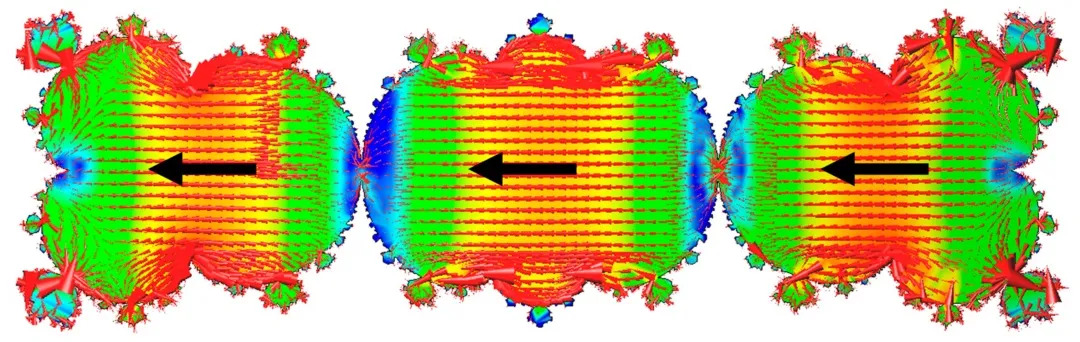
使用矩码的方法模拟电流分布 (f = 2.75 GHz), 黑色箭头 (有意添加) 表示天线表面的主流电流。

分形几何已经被证明在许多学科中是有用的。在天线工程领域，分形几何用于设计小型多波段天线阵列和高方向性元件。本文概述了最重要的分形数学先驱者的历史背景，同时展示了分形图案是如何启发工程师设计天线的。

访问后方链接，阅读英文原文：https://www.mdpi.com/2504-3110/4/1/3

 

The Unexpected Fractal Signatures in Fibonacci Chains

斐波那契数列中的意外分形特征

Fang Fang et al.

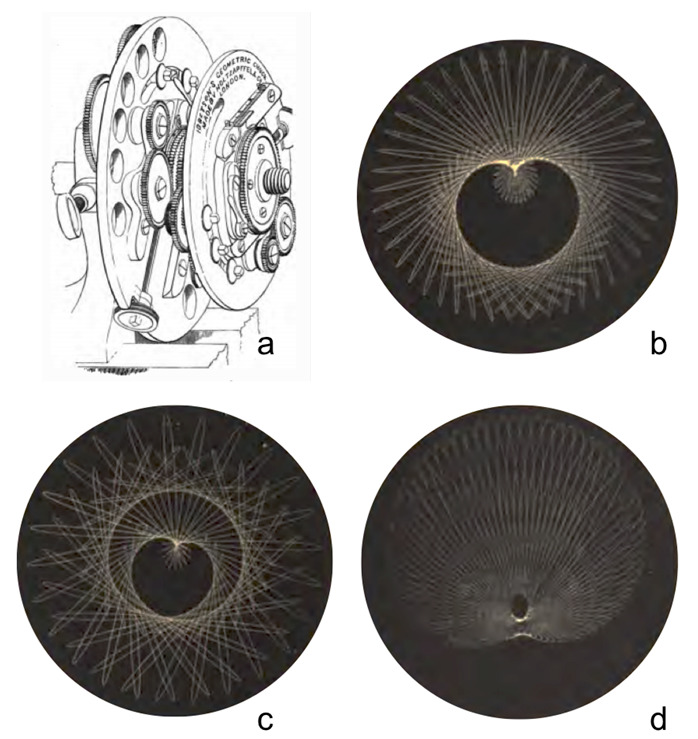
自从Shechtman于1982年发现准晶体后，它就引起了科学界的极大兴趣，因为准晶体具有奇特的、偶然反常的性质。这篇文章最为有趣的是，作者指出了准晶体的自相似性，这将它们与分形联系起来。前人对准结晶性质分形方面的研究主要围绕光谱和波函数分析展开，而对准晶体几何结构的数学研究较少。而本文介绍了一种分析准晶体分形特性的新框架，作者在斐波那契数列的傅里叶空间中展示了一个具有Mandelbrot集合的心形形状的新分形特征。在Fibonacci链上进行了各种修改，例如截断头或尾，打乱序列的顺序，改变L和S的比例，结果表明，分形特征对斐波那契数列的变化非常敏感，而对L/S比不敏感。

访问后方链接，阅读英文原文：https://www.mdpi.com/2504-3110/3/4/49

 

Cornu Spirals and the Triangular Lacunary Trigonometric System

角形螺旋和三角形的缺项三角系统

Trenton Vogt et al.

本文旨在补充Coutsias和Kazarinoff在1987年发表的一项非常有趣的研究，即缺项三角系统及其与菲涅耳积分的关系，特别是角形螺旋，这些系统与不完全高斯求和密切相关。目前的工作聚焦于建立在三角形数的特定系统。三角形数的特殊循环特性也体现在三角形的缺项三角系统中。具体地说，这一工作描述了由三角形的缺项三角系统产生的角形螺旋的特征，提出并讨论了自相似性、等距性和对称性等特殊特征。

访问后方链接，阅读英文原文：https://www.mdpi.com/2504-3110/3/3/40

 

Julia and Mandelbrot Sets for Dynamics over the Hyperbolic Numbers

用于双曲数字上的动力学的Julia和Mandelbrot集合

Vance Blankers et al.

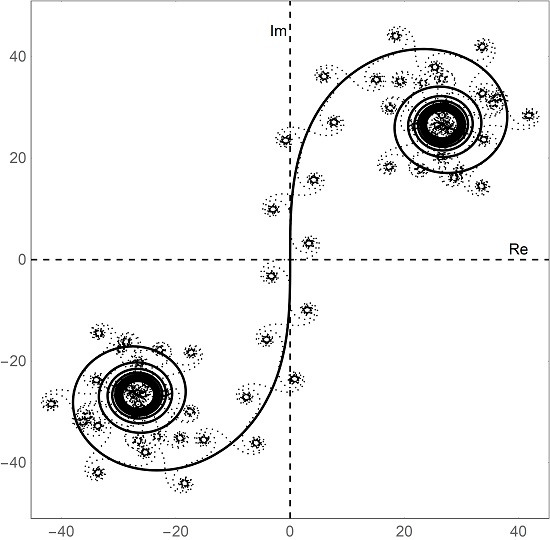
Julia和Mandelbrot集合，描述了复数上的动力学系统的有界轨道，是分形集合的经典例子。本文研究了这些集合在双曲数上的动力学系统的类比。双曲数字 (x+τy，其中x,y∈R, τ2=1但τ≠±1) 是编码Minkowski空间R1,1几何性质的自然数字系统。作者分析表明Mandelbrot集合的双曲类比使双曲Julia集合的连通性参数化，并给出了双曲平面的壁室分解。

访问后方链接，阅读英文原文：https://www.mdpi.com/2504-3110/3/1/6

 

版权声明：

本文作者：Fractal and Fractional Editorial Office

本文内容由MDPI中国办公室编辑负责撰写。如需转载，请邮件联系：mdpicnmarketing@mdpi.com